
Δευτέρα 17 Απριλίου 2017
Παρασκευή 14 Απριλίου 2017
Βέλτιστη γωνία παρατήρησης εικόνας
(84) Βέλτιστη γωνία παρατήρησης εικόνας - mathematica.gr
Τις ημέρες αυτές πλήθος κόσμου επισκέπτεται την εκκλησία, προσκυνά και κάποιοι παρατηρούν τις εικόνες ή τις τοιχογραφίες.
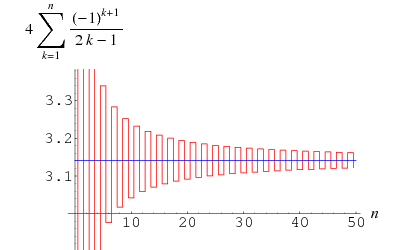
Ας υποθέσουμε ότι μία εικόνα, μήκους 1 μέτρου, βρίσκεται (το κάτω μέρος της) σε ύψος μέτρα από το έδαφος και ένας προσκυνητής, του οποίου τα μάτια βρίσκονται σε ύψος 1,8 μέτρα από το έδαφος παρατηρεί την εικόνα.
μέτρα από το έδαφος και ένας προσκυνητής, του οποίου τα μάτια βρίσκονται σε ύψος 1,8 μέτρα από το έδαφος παρατηρεί την εικόνα.
Να βρεθεί η θέση του παρατηρητή, ώστε η γωνία παρατήρησης της εικόνας (γωνία άνω μέρους, οφθαλμών, κάτω μέρους) να γίνει μέγιστη.
(γωνία άνω μέρους, οφθαλμών, κάτω μέρους) να γίνει μέγιστη.
#Regiomontanus, #Τέμνουσες κύκλου, #Εφαπτόμενος κύκλος
Τις ημέρες αυτές πλήθος κόσμου επισκέπτεται την εκκλησία, προσκυνά και κάποιοι παρατηρούν τις εικόνες ή τις τοιχογραφίες.
Ας υποθέσουμε ότι μία εικόνα, μήκους 1 μέτρου, βρίσκεται (το κάτω μέρος της) σε ύψος
 μέτρα από το έδαφος και ένας προσκυνητής, του οποίου τα μάτια βρίσκονται σε ύψος 1,8 μέτρα από το έδαφος παρατηρεί την εικόνα.
μέτρα από το έδαφος και ένας προσκυνητής, του οποίου τα μάτια βρίσκονται σε ύψος 1,8 μέτρα από το έδαφος παρατηρεί την εικόνα. Να βρεθεί η θέση του παρατηρητή, ώστε η γωνία παρατήρησης της εικόνας
 (γωνία άνω μέρους, οφθαλμών, κάτω μέρους) να γίνει μέγιστη.
(γωνία άνω μέρους, οφθαλμών, κάτω μέρους) να γίνει μέγιστη.#Regiomontanus, #Τέμνουσες κύκλου, #Εφαπτόμενος κύκλος
Τρίτη 4 Απριλίου 2017
Pi Formulas -- from Wolfram MathWorld - Προσεγγίζοντας το π
Pi Formulas -- from Wolfram MathWorld

There are many formulas of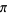 of many types. Among others, these include
of many types. Among others, these include
series, products, geometric constructions, limits, special values, and pi
iterations.
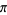 is intimately related to the properties of circles
is intimately related to the properties of circles
and spheres. For a circle of radius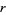 , the circumference
, the circumference
and area are given by
Similarly, for a sphere of radius 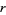 , the surface area
, the surface area
and volume enclosed are
An exact formula for 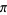 in terms of the inverse
in terms of the inverse
tangents of unit fractions is Machin's
formula
There are three other Machin-like formulas,
as well as thousands of other similar formulas having more terms.
Gregory and Leibniz found
(Wells 1986, p. 50), which is known as the Gregory series and may be obtained by plugging 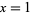 into the Leibniz series for
into the Leibniz series for 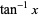 . The error
. The error
after the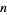 th term of this series in the Gregory
th term of this series in the Gregory
series is larger than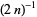 so this sum converges so slowly
so this sum converges so slowly
that 300 terms are not sufficient to calculate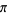 correctly to two
correctly to two
decimal places! However, it can be transformed to
where 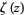 is the Riemann
is the Riemann
zeta function (Vardi 1991, pp. 157-158; Flajolet and Vardi 1996), so that
the error after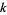 terms is
terms is 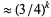 .
.
An infinite sum series to Abraham Sharp (ca. 1717) is given by
(Smith 1953, p. 311). Additional simple series in which 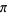 appears are
appears are
(Wells 1986, p. 53).
In 1666, Newton used a geometric construction to derive the formula
which he used to compute 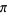 (Wells 1986, p. 50; Borwein et
(Wells 1986, p. 50; Borwein et
al. 1989; Borwein and Bailey 2003, pp. 105-106). The coefficients can be
found from the integral
by taking the series expansion of 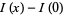 about
about
0, obtaining
(OEIS A054387 and A054388). Using Euler's convergence improvement
transformation gives
(Beeler et al. 1972, Item 120).
This corresponds to plugging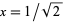 into
into
the power series for the hypergeometric
function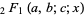 ,
,
Despite the convergence improvement, series (◇) converges at only one bit/term. At the cost of a square root, Gosper has noted that
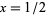 gives 2 bits/term,
gives 2 bits/term,
and 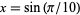 gives almost 3.39 bits/term,
gives almost 3.39 bits/term,
where 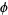 is the golden
is the golden
ratio. Gosper also obtained
A spigot algorithm for 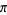 is given by Rabinowitz
is given by Rabinowitz
and Wagon (1995; Borwein and Bailey 2003, pp. 141-142).
More amazingly still, a closed form expression giving a digit-extraction algorithm which produces digits of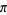 (or
(or 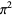 ) in base-16
) in base-16
was discovered by Bailey et al. (Bailey et al. 1997, Adamchik and Wagon
1997),
This formula, known as the BBP formula, was discovered using the PSLQ algorithm (Ferguson et al. 1999)
and is equivalent to
There is a series of BBP-type formulas for 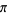 in powers of
in powers of 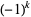 , the first
, the first
few independent formulas of which are
Similarly, there are a series of BBP-type formulas for 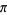 in powers of
in powers of 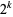 , the first few
, the first few
independent formulas of which are
F. Bellard found the rapidly converging BBP-type
formula
A related integral is
(Dalzell 1944, 1971; Le Lionnais 1983, p. 22; Borwein, Bailey, and
Girgensohn 2004, p. 3; Boros and Moll 2004, p. 125; Lucas 2005; Borwein et al.
2007, p. 14). This integral was known by K. Mahler in the mid-1960s
and appears in an exam at the University of Sydney in November 1960 (Borwein, Bailey,
and Girgensohn, p. 3). Beukers (2000) and Boros and Moll (2004, p. 126)
state that it is not clear if these exists a natural choice of rational polynomial
whose integral between 0 and 1 produces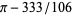 , where
, where
333/106 is the next convergent. However, an integral exists for the fourth
convergent, namely
(Lucas 2005; Bailey et al. 2007, p. 219). In fact, Lucas (2005) gives
a few other such integrals.
Backhouse (1995) used the identity
for positive integer 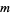 and
and 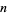 and where
and where 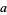 ,
, 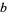 , and
, and 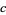 are rational constant
are rational constant
to generate a number of formulas for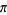 . In particular,
. In particular,
if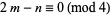 , then
, then 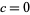 (Lucas 2005).
(Lucas 2005).
A similar formula was subsequently discovered by Ferguson, leading to a
two-dimensional lattice of such formulas which can be generated by these
two formulas given by
for any complex value of 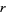 (Adamchik and Wagon), giving the BBP
(Adamchik and Wagon), giving the BBP
formula as the special case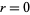 .
.
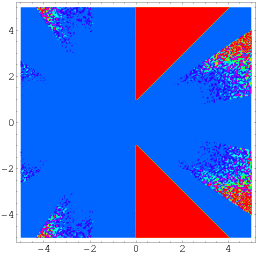
An even more general identity due to Wagon is given by
(Borwein and Bailey 2003, p. 141), which holds over a region of the complex plane excluding two triangular portions symmetrically placed about the real
axis, as illustrated above.
A perhaps even stranger general class of identities is given by
which holds for any positive integer 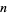 , where
, where 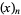 is a Pochhammer
is a Pochhammer
symbol (B. Cloitre, pers. comm., Jan. 23, 2005). Even more amazingly,
there is a closely analogous formula for the natural
logarithm of 2.
Following the discovery of the base-16 digit BBP formula and related formulas, similar formulas in other bases were investigated. Borwein,
Bailey, and Girgensohn (2004) have recently shown that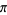 has no Machin-type
has no Machin-type
BBP arctangent formula that is not binary, although this does not rule out a completely
different scheme for digit-extraction algorithms
in other bases.
S. Plouffe has devised an algorithm to compute the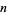 th digit
th digit
of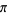 in any base in
in any base in 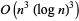 steps.
steps.
A slew of additional identities due to Ramanujan, Catalan, and Newton
are given by Castellanos (1988ab, pp. 86-88), including several
involving sums of Fibonacci
numbers. Ramanujan found
(Hardy 1923, 1924, 1999, p. 7).
Plouffe (2006) found the beautiful formula
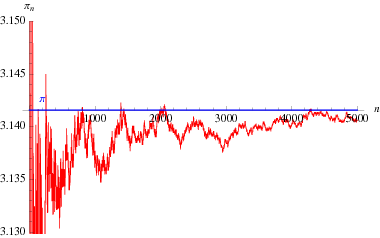
An interesting infinite product formula due to Euler which relates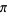 and the
and the 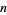 th prime
th prime 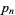 is
is
(Blatner 1997, p. 119), plotted above as a function of the number of terms in the product.
A method similar to Archimedes' can be used to estimate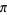 by starting with
by starting with
an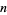 -gon and then relating the area
-gon and then relating the area
of subsequent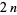 -gons. Let
-gons. Let 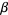 be the angle
be the angle
from the center of one of the polygon's segments,
then
(Beckmann 1989, pp. 92-94).
Vieta (1593) was the first to give an exact expression for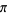 by taking
by taking 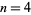 in the above expression, giving
in the above expression, giving
which leads to an infinite product of nested
radicals,
(Wells 1986, p. 50; Beckmann 1989, p. 95). However, this expression was not rigorously proved to converge until Rudio in 1892.
A related formula is given by
which can be written
where 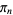 is defined using the iteration
is defined using the iteration
with 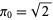 (J. Munkhammar, pers.
(J. Munkhammar, pers.
comm., April 27, 2000). The formula
is also closely related.
A pretty formula for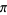 is given by
is given by
where the numerator is a form of the Wallis formula for 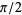 and the denominator is a telescoping
and the denominator is a telescoping
sum with sum 1/2 since
(Sondow 1997).
A particular case of the Wallis formula gives
(Wells 1986, p. 50). This formula can also be written
where 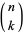 denotes a binomial
denotes a binomial
coefficient and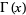 is the gamma
is the gamma
function (Knopp 1990). Euler obtained
which follows from the special value of the Riemann zeta function 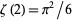 . Similar formulas
. Similar formulas
follow from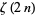 for all positive
for all positive
integers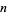 .
.
An infinite sum due to Ramanujan is
(Borwein et al. 1989; Borwein and Bailey 2003, p. 109; Bailey et al.
2007, p. 44). Further sums are given in Ramanujan (1913-14),
and
(Beeler et al. 1972, Item 139; Borwein et al. 1989; Borwein and Bailey 2003, p. 108; Bailey et al. 2007, p. 44). Equation (78)
is derived from a modular identity of order 58, although a first derivation was not
presented prior to Borwein and Borwein (1987). The above series both give
(Wells 1986, p. 54) as the first approximation and provide,
respectively, about 6 and 8 decimal places per term. Such series exist
because of the rationality of various modular invariants.
The general form of the series is
where 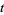 is a binary
is a binary
quadratic form discriminant,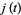 is the j-function,
is the j-function,
and the 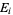 are Eisenstein
are Eisenstein
series. A class number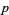 field involves
field involves
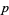 th degree algebraic
th degree algebraic
integers of the constants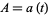 ,
, 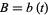 , and
, and 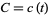 . Of all series consisting of only integer
. Of all series consisting of only integer
terms, the one gives the most numeric digits in the shortest period of time corresponds
to the largest class number 1 discriminant of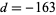 and was formulated by the Chudnovsky brothers
and was formulated by the Chudnovsky brothers
(1987). The 163 appearing here is the same one appearing in the fact that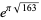
(the Ramanujan constant) is very nearly an
integer. Similarly, the factor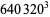 comes from
comes from
the j-function identity for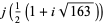 .
.
The series is given by
(Borwein and Borwein 1993; Beck and Trott; Bailey et al. 2007, p. 44). This series gives 14 digits accurately per term. The same equation in another form
was given by the Chudnovsky brothers (1987) and is used by the Wolfram
Language to calculate (Vardi 1991; Wolfram Research),
(Vardi 1991; Wolfram Research),
where
The best formula for class number 2 (largest discriminant  ) is
) is
where
(Borwein and Borwein 1993). This series adds about 25 digits for each additional term. The fastest converging series for class number
3 corresponds to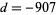 and gives 37-38 digits per term.
and gives 37-38 digits per term.
The fastest converging class number 4 series corresponds
to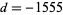 and is
and is
where
This gives 50 digits per term. Borwein and Borwein (1993) have developed a general algorithm for generating such series for arbitrary
class number.
A complete listing of Ramanujan's series for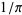 found in his
found in his
second and third notebooks is given by Berndt (1994, pp. 352-354),
These equations were first proved by Borwein and Borwein (1987a,
pp. 177-187). Borwein and Borwein (1987b, 1988, 1993) proved other
equations of this type, and
Chudnovsky and Chudnovsky (1987) found similar equations for other
transcendental
constants (Bailey et al. 2007, pp. 44-45).
A complete list of independent known equations of this type is given by
for 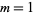 with nonalternating signs,
with nonalternating signs,
for 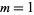 with alternating signs,
with alternating signs,
for 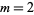 (Guillera 2002, 2003, 2006),
(Guillera 2002, 2003, 2006),
for 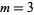 (Guillera 2002, 2003, 2006), and no others for
(Guillera 2002, 2003, 2006), and no others for
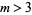 are known (Bailey et al. 2007, pp. 45-48).
are known (Bailey et al. 2007, pp. 45-48).
Bellard gives the exotic formula
where
Gasper quotes the result
where 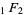 is a generalized
is a generalized
hypergeometric function, and transforms it to
A fascinating result due to Gosper is given by
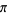 satisfies the inequality
satisfies the inequality
D. Terr (pers. comm.) noted the curious identity
involving the first 9 digits of pi.
SEE ALSO: BBP Formula, Digit-Extraction Algorithm, Pi, Pi Approximations,
Pi Continued Fraction, Pi
Digits, Pi Iterations, Pi
Squared, Spigot Algorithm
REFERENCES:
CITE THIS AS:
Pi Formulas
There are many formulas of
series, products, geometric constructions, limits, special values, and pi
iterations.
and spheres. For a circle of radius
and area are given by
(1) | |||
(2) |
and volume enclosed are
(3) | |||
(4) |
tangents of unit fractions is Machin's
formula
(5) |
as well as thousands of other similar formulas having more terms.

Gregory and Leibniz found
(6) | |||
(7) |
after the
series is larger than
that 300 terms are not sufficient to calculate
decimal places! However, it can be transformed to
(8) |
zeta function (Vardi 1991, pp. 157-158; Flajolet and Vardi 1996), so that
the error after
An infinite sum series to Abraham Sharp (ca. 1717) is given by
(9) |
(10) | |||
(11) | |||
(12) | |||
(13) | |||
(14) | |||
(15) | |||
(16) | |||
(17) |
In 1666, Newton used a geometric construction to derive the formula
(18) | |||
(19) |
al. 1989; Borwein and Bailey 2003, pp. 105-106). The coefficients can be
found from the integral
(20) | |||
(21) |
0, obtaining
(22) |
transformation gives
(23) | |||
(24) | |||
(25) |
This corresponds to plugging
the power series for the hypergeometric
function
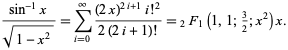 | (26) |
(27) |
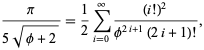 | (28) |
ratio. Gosper also obtained
(29) |
and Wagon (1995; Borwein and Bailey 2003, pp. 141-142).
More amazingly still, a closed form expression giving a digit-extraction algorithm which produces digits of
was discovered by Bailey et al. (Bailey et al. 1997, Adamchik and Wagon
1997),
(30) |
and is equivalent to
(31) |
few independent formulas of which are
(32) | |||
(33) | |||
(34) | |||
![sum_(k=0)^(infty)(-1)^k[3/(14k+1)-3/(14k+3)+3/(14k+5)+4/(14k+7)+4/(14k+9)-4/(14k+11)+4/(14k+13)]](http://mathworld.wolfram.com/images/equations/PiFormulas/Inline101.gif) | (35) | ||
![sum_(k=0)^(infty)(-1)^k[2/(18k+1)+3/(18k+3)+2/(18k+5)-2/(18k+7)-2/(18k+11)+2/(18k+13)+3/(18k+15)+2/(18k+17)]](http://mathworld.wolfram.com/images/equations/PiFormulas/Inline104.gif) | (36) | ||
![sum_(k=0)^(infty)(-1)^k[3/(22k+1)-3/(22k+3)+3/(22k+5)-3/(22k+7)+3/(22k+9)+8/(22k+11)+3/(22k+13)-3/(22k+15)+3/(22k+17)-3/(22k+19)+1/(22k+21)].](http://mathworld.wolfram.com/images/equations/PiFormulas/Inline107.gif) | (37) |
independent formulas of which are
(38) | |||
(39) | |||
![1/(16)sum_(k=0)^(infty)1/(256^k)[(64)/(16k+1)-(32)/(16k+4)-(16)/(16k+5)-(16)/(16k+6)+4/(16k+9)-2/(16k+12)-1/(16k+13)-1/(16k+14)]](http://mathworld.wolfram.com/images/equations/PiFormulas/Inline118.gif) | (40) | ||
![1/(32)sum_(k=0)^(infty)1/(256^k)[(128)/(16k+2)+(64)/(16k+3)+(64)/(16k+4)-(16)/(16k+7)+8/(16k+10)+4/(16k+11)+4/(16k+12)-1/(16k+15)]](http://mathworld.wolfram.com/images/equations/PiFormulas/Inline121.gif) | (41) | ||
![1/(32)sum_(k=0)^(infty)1/(4096^k)[(256)/(24k+2)+(192)/(24k+3)-(256)/(24k+4)-(96)/(24k+6)-(96)/(24k+8)+(16)/(24k+10)-4/(24k+12)-3/(24k+15)-6/(24k+16)-2/(24k+18)-1/(24k+20)]](http://mathworld.wolfram.com/images/equations/PiFormulas/Inline124.gif) | (42) | ||
![1/(64)sum_(k=0)^(infty)1/(4096^k)[(256)/(24k+1)+(256)/(24k+2)-(384)/(24k+3)-(256)/(24k+4)-(64)/(24k+5)+(96)/(24k+8)+(64)/(24k+9)+(16)/(24k+10)+8/(24k+12)-4/(24k+13)+6/(24k+15)+6/(24k+16)+1/(24k+17)+1/(24k+18)-1/(24k+20)-1/(24k+21)]](http://mathworld.wolfram.com/images/equations/PiFormulas/Inline127.gif) | (43) | ||
![1/(96)sum_(k=0)^(infty)1/(4096^k)[(256)/(24k+2)+(64)/(24k+3)+(128)/(24k+5)+(352)/(24k+6)+(64)/(24k+7)+(288)/(24k+8)+(128)/(24k+9)+(80)/(24k+10)+(20)/(24k+12)-(16)/(24k+14)-1/(24k+15)+6/(24k+16)-2/(24k+17)-1/(24k+19)+1/(24k+20)-2/(24k+21)]](http://mathworld.wolfram.com/images/equations/PiFormulas/Inline130.gif) | (44) | ||
![1/(96)sum_(k=0)^(infty)1/(4096^k)[(256)/(24k+1)+(320)/(24k+3)+(256)/(24k+4)-(192)/(24k+5)-(224)/(24k+6)-(64)/(24k+7)-(192)/(24k+8)-(64)/(24k+9)-(64)/(24k+10)-(28)/(24k+12)-4/(24k+13)-5/(24k+15)+3/(24k+17)+1/(24k+18)+1/(24k+19)+1/(24k+21)-1/(24k+22)]](http://mathworld.wolfram.com/images/equations/PiFormulas/Inline133.gif) | (45) | ||
![1/(96)sum_(k=0)^(infty)1/(4096^k)[(512)/(24k+1)-(256)/(24k+2)+(64)/(24k+3)-(512)/(24k+4)-(32)/(24k+6)+(64)/(24k+7)+(96)/(24k+8)+(64)/(24k+9)+(48)/(24k+10)-(12)/(24k+12)-8/(24k+13)-(16)/(24k+14)-1/(24k+15)-6/(24k+16)-2/(24k+18)-1/(24k+19)-1/(24k+20)-1/(24k+21)]](http://mathworld.wolfram.com/images/equations/PiFormulas/Inline136.gif) | (46) | ||
![1/(4096)sum_(k=0)^(infty)1/(65536^k)[(16384)/(32k+1)-(8192)/(32k+4)-(4096)/(32k+5)-(4096)/(32k+6)+(1024)/(32k+9)-(512)/(32k+12)-(256)/(32k+13)-(256)/(32k+14)+(64)/(32k+17)-(32)/(32k+20)-(16)/(32k+21)-(16)/(32k+22)+4/(32k+25)-2/(32k+28)-1/(32k+29)-1/(32k+30)]](http://mathworld.wolfram.com/images/equations/PiFormulas/Inline139.gif) | (47) | ||
![1/(4096)sum_(k=0)^(infty)1/(65536^k)[(32768)/(32k+2)+(16384)/(32k+3)+(16384)/(32k+4)-(4096)/(32k+7)+(2048)/(32k+10)+(1024)/(32k+11)+(1024)/(32k+12)-(256)/(32k+15)+(128)/(32k+18)+(64)/(32k+19)+(64)/(32k+20)-(16)/(32k+23)+8/(32k+26)+4/(32k+27)+4/(32k+28)-1/(32k+31)].](http://mathworld.wolfram.com/images/equations/PiFormulas/Inline142.gif) | (48) |
formula
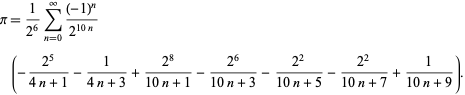 | (49) |
(50) |
Girgensohn 2004, p. 3; Boros and Moll 2004, p. 125; Lucas 2005; Borwein et al.
2007, p. 14). This integral was known by K. Mahler in the mid-1960s
and appears in an exam at the University of Sydney in November 1960 (Borwein, Bailey,
and Girgensohn, p. 3). Beukers (2000) and Boros and Moll (2004, p. 126)
state that it is not clear if these exists a natural choice of rational polynomial
whose integral between 0 and 1 produces
333/106 is the next convergent. However, an integral exists for the fourth
convergent, namely
(51) |
a few other such integrals.
Backhouse (1995) used the identity
(52) | |||
(53) | |||
(54) |
to generate a number of formulas for
if
A similar formula was subsequently discovered by Ferguson, leading to a
two-dimensional lattice of such formulas which can be generated by these
two formulas given by
(55) |
formula as the special case

An even more general identity due to Wagon is given by
![pi+4tan^(-1)z+2ln((1-2z-z^2)/(z^2+1))=sum_(k=0)^infty1/(16^k)[(4(z+1)^(8k+1))/(8k+1)-(2(z+1)^(8k+4))/(8k+4)-((z+1)^(8k+5))/(8k+5)-((z+1)^(8k+6))/(8k+6)]](http://mathworld.wolfram.com/images/equations/PiFormulas/NumberedEquation15.gif) | (56) |
axis, as illustrated above.
A perhaps even stranger general class of identities is given by
![pi=4sum_(j=1)^n((-1)^(j+1))/(2j-1)+((-1)^n(2n-1)!)/4sum_(k=0)^infty1/(16^k)[8/((8k+1)_(2n))-4/((8k+3)_(2n))-4/((8k+4)_(2n))-2/((8k+5)_(2n))+1/((8k+7)_(2n))+1/((8k+8)_(2n))]](http://mathworld.wolfram.com/images/equations/PiFormulas/NumberedEquation16.gif) | (57) |
symbol (B. Cloitre, pers. comm., Jan. 23, 2005). Even more amazingly,
there is a closely analogous formula for the natural
logarithm of 2.
Following the discovery of the base-16 digit BBP formula and related formulas, similar formulas in other bases were investigated. Borwein,
Bailey, and Girgensohn (2004) have recently shown that
BBP arctangent formula that is not binary, although this does not rule out a completely
different scheme for digit-extraction algorithms
in other bases.
S. Plouffe has devised an algorithm to compute the
of
A slew of additional identities due to Ramanujan, Catalan, and Newton
are given by Castellanos (1988ab, pp. 86-88), including several
involving sums of Fibonacci
numbers. Ramanujan found
![sum_(k=0)^infty((-1)^k(4k+1)[(2k-1)!!]^3)/([(2k)!!]^3)=sum_(k=0)^infty((-1)^k(4k+1)[Gamma(k+1/2)]^3)/(pi^(3/2)[Gamma(k+1)]^3)=2/pi](http://mathworld.wolfram.com/images/equations/PiFormulas/NumberedEquation17.gif) | (58) |
Plouffe (2006) found the beautiful formula
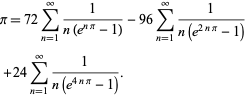 | (59) |

An interesting infinite product formula due to Euler which relates
![2/(product_(n=1)^(infty)[1+(sin(1/2pip_n))/(p_n)])](http://mathworld.wolfram.com/images/equations/PiFormulas/Inline174.gif) | (60) | ||
(61) |
A method similar to Archimedes' can be used to estimate
an
of subsequent
from the center of one of the polygon's segments,
(62) |
(63) |
Vieta (1593) was the first to give an exact expression for
(64) |
radicals,
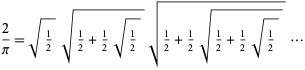 | (65) |
A related formula is given by
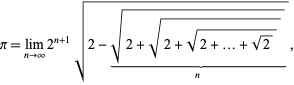 | (66) |
(67) |
![pi_n=sqrt((1/2pi_(n-1))^2+[1-sqrt(1-(1/2pi_(n-1))^2)]^2)](http://mathworld.wolfram.com/images/equations/PiFormulas/NumberedEquation25.gif) | (68) |
comm., April 27, 2000). The formula
![pi=2lim_(m->infty)sum_(n=1)^msqrt([sqrt(1-((n-1)/m)^2)-sqrt(1-(n/m)^2)]^2+1/(m^2))](http://mathworld.wolfram.com/images/equations/PiFormulas/NumberedEquation26.gif) | (69) |
A pretty formula for
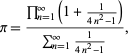 | (70) |
sum with sum 1/2 since
(71) |
A particular case of the Wallis formula gives
(72) |
![lim_(n->infty)(2^(4n))/(n(2n; n)^2)=pilim_(n->infty)(n[Gamma(n)]^2)/([Gamma(1/2+n)]^2)=pi,](http://mathworld.wolfram.com/images/equations/PiFormulas/NumberedEquation30.gif) | (73) |
coefficient and
function (Knopp 1990). Euler obtained
(74) |
follow from
integers
An infinite sum due to Ramanujan is
(75) |
2007, p. 44). Further sums are given in Ramanujan (1913-14),
(76) |
(77) | |||
(78) |
is derived from a modular identity of order 58, although a first derivation was not
presented prior to Borwein and Borwein (1987). The above series both give
(79) |
respectively, about 6 and 8 decimal places per term. Such series exist
because of the rationality of various modular invariants.
The general form of the series is
(80) |
quadratic form discriminant,
(81) | |||
(82) |
series. A class number
integers of the constants
terms, the one gives the most numeric digits in the shortest period of time corresponds
to the largest class number 1 discriminant of
(1987). The 163 appearing here is the same one appearing in the fact that
(the Ramanujan constant) is very nearly an
integer. Similarly, the factor
the j-function identity for
The series is given by
(83) | |||
(84) |
was given by the Chudnovsky brothers (1987) and is used by the Wolfram
Language to calculate
(85) |
(86) | |||
(87) | |||
(88) |
(89) |
(90) | |||
(91) | |||
(92) |
3 corresponds to
The fastest converging class number 4 series corresponds
to
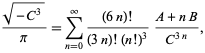 | (93) |
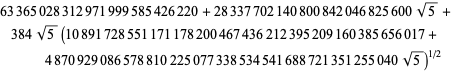 | (94) | ||
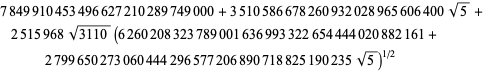 | (95) | ||
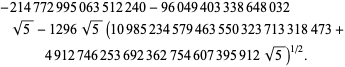 | (96) |
class number.
A complete listing of Ramanujan's series for
second and third notebooks is given by Berndt (1994, pp. 352-354),
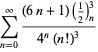 | (97) | ||
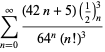 | (98) | ||
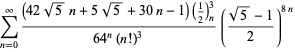 | (99) | ||
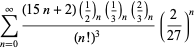 | (100) | ||
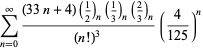 | (101) | ||
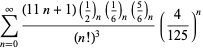 | (102) | ||
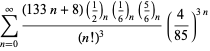 | (103) | ||
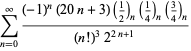 | (104) | ||
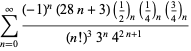 | (105) | ||
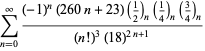 | (106) | ||
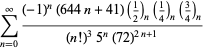 | (107) | ||
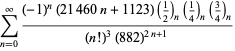 | (108) | ||
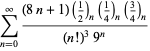 | (109) | ||
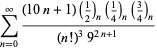 | (110) | ||
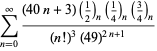 | (111) | ||
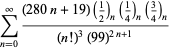 | (112) | ||
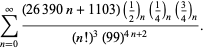 | (113) |
pp. 177-187). Borwein and Borwein (1987b, 1988, 1993) proved other
equations of this type, and
Chudnovsky and Chudnovsky (1987) found similar equations for other
transcendental
constants (Bailey et al. 2007, pp. 44-45).
A complete list of independent known equations of this type is given by
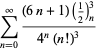 | (114) | ||
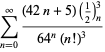 | (115) | ||
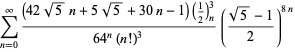 | (116) | ||
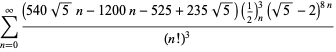 | (117) | ||
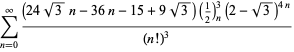 | (118) |
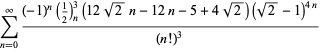 | (119) | ||
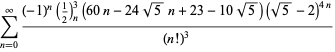 | (120) | ||
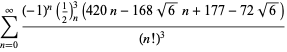 | (121) | ||
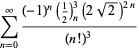 | (122) |
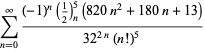 | (123) | ||
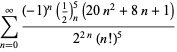 | (124) |
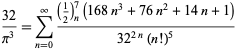 | (125) |
Bellard gives the exotic formula
![pi=1/(740025)[sum_(n=1)^infty(3P(n))/((7n; 2n)2^(n-1))-20379280],](http://mathworld.wolfram.com/images/equations/PiFormulas/NumberedEquation40.gif) | (126) |
(127) |
(128) |
hypergeometric function, and transforms it to
(129) |
(130) |
(131) |
(132) |
SEE ALSO: BBP Formula, Digit-Extraction Algorithm, Pi, Pi Approximations,
Pi Continued Fraction, Pi
Digits, Pi Iterations, Pi
Squared, Spigot Algorithm
REFERENCES:
Adamchik, V. and Wagon, S. "A Simple Formula for 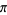 ." Amer.
." Amer.
Math. Monthly 104, 852-855, 1997.
Math. Monthly 104, 852-855, 1997.
Adamchik, V. and Wagon, S. "Pi: A 2000-Year Search Changes Direction."
http://www-2.cs.cmu.edu/~adamchik/articles/pi.htm.
http://www-2.cs.cmu.edu/~adamchik/articles/pi.htm.
Backhouse, N. "Note 79.36. Pancake Functions and Approximations to 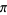 ." Math.
." Math.
Gaz. 79, 371-374, 1995.
Gaz. 79, 371-374, 1995.
Bailey, D. H. "Numerical Results on the Transcendence of Constants Involving 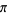 ,
, 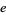 , and Euler's Constant."
, and Euler's Constant."
Math. Comput. 50, 275-281, 1988a.
Math. Comput. 50, 275-281, 1988a.
Bailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn, R.; Luke, D. R.; and Moll, V. H. Experimental
Mathematics in Action. Wellesley, MA: A K Peters, 2007.
Mathematics in Action. Wellesley, MA: A K Peters, 2007.
Bailey, D. H.; Borwein, P.; and Plouffe, S. "On the Rapid Computation of Various Polylogarithmic Constants." Math. Comput. 66, 903-913,
1997.
1997.
Beck, G. and Trott, M. "Calculating Pi: From Antiquity to Moderns Times."
http://documents.wolfram.com/mathematica/Demos/Notebooks/CalculatingPi.html.
http://documents.wolfram.com/mathematica/Demos/Notebooks/CalculatingPi.html.
Beckmann, P. A
History of Pi, 3rd ed. New York: Dorset Press, 1989.
History of Pi, 3rd ed. New York: Dorset Press, 1989.
Beeler, M. et al. Item 140 in Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239,
p. 69, Feb. 1972. http://www.inwap.com/pdp10/hbaker/hakmem/pi.html#item140.
p. 69, Feb. 1972. http://www.inwap.com/pdp10/hbaker/hakmem/pi.html#item140.
Berndt, B. C. Ramanujan's
Notebooks, Part IV. New York: Springer-Verlag, 1994.
Notebooks, Part IV. New York: Springer-Verlag, 1994.
Beukers, F. "A Rational Approximation to 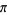 ." Nieuw
." Nieuw
Arch. Wisk. 5, 372-379, 2000.
Arch. Wisk. 5, 372-379, 2000.
Blatner, D. The
Joy of Pi. New York: Walker, 1997.
Joy of Pi. New York: Walker, 1997.
Boros, G. and Moll, V. Irresistible Integrals: Symbolics, Analysis and Experiments in the Evaluation of Integrals.
Cambridge, England: Cambridge University Press, 2004.
Cambridge, England: Cambridge University Press, 2004.
Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A
K Peters, 2003.
K Peters, 2003.
Borwein, J.; Bailey, D.; and Girgensohn, R. Experimentation in Mathematics: Computational Paths to Discovery. Wellesley, MA: A K Peters,
2004.
2004.
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity.
New York: Wiley, 1987a.
New York: Wiley, 1987a.
Borwein, J. M. and Borwein, P. B. "Ramanujan's Rational and Algebraic Series for 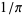 ." Indian J. Math. 51,
." Indian J. Math. 51,
147-160, 1987b.
147-160, 1987b.
Borwein, J. M. and Borwein, P. B. "More Ramanujan-Type Series for 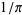 ." In Ramanujan
." In Ramanujan
Revisited: Proceedings of the Centenary Conference, University of Illinois at Urbana-Champaign,
June 1-5, 1987 (Ed. G. E. Andrews, B. C. Berndt, and
R. A. Rankin). New York: Academic Press, pp. 359-374, 1988.
Revisited: Proceedings of the Centenary Conference, University of Illinois at Urbana-Champaign,
June 1-5, 1987 (Ed. G. E. Andrews, B. C. Berndt, and
R. A. Rankin). New York: Academic Press, pp. 359-374, 1988.
Borwein, J. M. and Borwein, P. B. "Class Number Three Ramanujan Type Series for 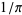 ." J. Comput. Appl. Math. 46,
." J. Comput. Appl. Math. 46,
281-290, 1993.
281-290, 1993.
Borwein, J. M.; Borwein, P. B.; and Bailey, D. H. "Ramanujan, Modular
Equations, and Approximations to Pi, or How to Compute One Billion
Digits
of Pi." Amer. Math. Monthly 96, 201-219, 1989.
Equations, and Approximations to Pi, or How to Compute One Billion
Digits
of Pi." Amer. Math. Monthly 96, 201-219, 1989.
Borwein, J. M.; Borwein, D.; and Galway, W. F. "Finding and Excluding 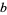 -ary Machin-Type Individual Digit Formulae."
-ary Machin-Type Individual Digit Formulae."
Canad. J. Math. 56, 897-925, 2004.
Canad. J. Math. 56, 897-925, 2004.
Castellanos, D. "The Ubiquitous Pi. Part I." Math. Mag. 61,
67-98, 1988a.
67-98, 1988a.
Castellanos, D. "The Ubiquitous Pi. Part II." Math. Mag. 61,
148-163, 1988b.
148-163, 1988b.
Chudnovsky, D. V. and Chudnovsky, G. V. "Approximations and Complex Multiplication According to Ramanujan." In Ramanujan
Revisited: Proceedings of the Centenary Conference, University of Illinois at Urbana-Champaign,
June 1-5, 1987 (Ed. G. E. Andrews, B. C. Berndt, and
R. A. Rankin). Boston, MA: Academic Press, pp. 375-472, 1987.
Revisited: Proceedings of the Centenary Conference, University of Illinois at Urbana-Champaign,
June 1-5, 1987 (Ed. G. E. Andrews, B. C. Berndt, and
R. A. Rankin). Boston, MA: Academic Press, pp. 375-472, 1987.
Dalzell, D. P. "On 22/7." J. London Math. Soc. 19, 133-134,
1944.
1944.
Dalzell, D. P. "On 22/7 and 355/113." Eureka 34, 10-13,
1971.
1971.
Ferguson, H. R. P.; Bailey, D. H.; and Arno, S. "Analysis of PSLQ, An Integer Relation Finding Algorithm." Math. Comput. 68,
351-369, 1999.
351-369, 1999.
Finch, S. R. Mathematical
Constants. Cambridge, England: Cambridge University Press, 2003.
Constants. Cambridge, England: Cambridge University Press, 2003.
Flajolet, P. and Vardi, I. "Zeta Function Expansions of Classical Constants."
Unpublished manuscript. 1996. http://algo.inria.fr/flajolet/Publications/landau.ps.
Unpublished manuscript. 1996. http://algo.inria.fr/flajolet/Publications/landau.ps.
Gasper, G. "Re: confluent pi." math-fun@cs.arizona.edu posting, Aug. 18, 1996.
Gosper, R. W. math-fun@cs.arizona.edu posting, Sept. 1996.
Gosper, R. W. "a product." math-fun@cs.arizona.edu posting,
Sept. 27, 1996.
Sept. 27, 1996.
Gourdon, X. and Sebah, P. "Collection of Series for 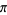 ." http://numbers.computation.free.fr/Constants/Pi/piSeries.html.
." http://numbers.computation.free.fr/Constants/Pi/piSeries.html.
Guillera, J. "Some Binomial Series Obtained by the WZ-Method." Adv.
Appl. Math. 29, 599-603, 2002.
Appl. Math. 29, 599-603, 2002.
Guillera, J. "About a New Kind of Ramanujan-Type Series." Exp. Math. 12,
507-510, 2003.
507-510, 2003.
Guillera, J. "Generators of Some Ramanujan Formulas." Ramanujan J. 11,
41-48, 2006.
41-48, 2006.
Hardy, G. H. "A Chapter from Ramanujan's Note-Book." Proc. Cambridge
Philos. Soc. 21, 492-503, 1923.
Philos. Soc. 21, 492-503, 1923.
Hardy, G. H. "Some Formulae of Ramanujan." Proc. London Math. Soc.
(Records of Proceedings at Meetings) 22, xii-xiii, 1924.
(Records of Proceedings at Meetings) 22, xii-xiii, 1924.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York:
Chelsea, 1999.
Chelsea, 1999.
Le Lionnais, F. Les
nombres remarquables. Paris: Hermann, 1983.
nombres remarquables. Paris: Hermann, 1983.
Lucas, S. K. "Integral Proofs that 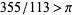 ."
."
Austral. Math. Soc. Gaz. 32, 263-266, 2005.
Austral. Math. Soc. Gaz. 32, 263-266, 2005.
MathPages. "Rounding Up to Pi." http://www.mathpages.com/home/kmath001.htm.
Plouffe, S. "Identities Inspired from Ramanujan Notebooks (Part 2)." Apr. 2006.
http://www.lacim.uqam.ca/~plouffe/inspired2.pdf.
http://www.lacim.uqam.ca/~plouffe/inspired2.pdf.
Rabinowitz, S. and Wagon, S. "A Spigot Algorithm for the Digits of 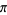 ." Amer.
." Amer.
Math. Monthly 102, 195-203, 1995.
Math. Monthly 102, 195-203, 1995.
Ramanujan, S. "Modular Equations and Approximations to 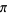 ." Quart.
." Quart.
J. Pure. Appl. Math. 45, 350-372, 1913-1914.
J. Pure. Appl. Math. 45, 350-372, 1913-1914.
Smith, D. History
of Mathematics, Vol. 2. New York: Dover, 1953.
of Mathematics, Vol. 2. New York: Dover, 1953.
Sondow, J. "Problem 88." Math Horizons, pp. 32 and 34, Sept. 1997.
Sondow, J. "A Faster Product for 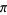 and a New Integral
and a New Integral
for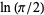 ." Amer. Math. Monthly 112,
." Amer. Math. Monthly 112,
729-734, 2005.
for
729-734, 2005.
Vardi, I. Computational
Recreations in Mathematica. Reading, MA: Addison-Wesley, p. 159, 1991.
Recreations in Mathematica. Reading, MA: Addison-Wesley, p. 159, 1991.
Vieta, F. Uriorum de rebus mathematicis responsorum. Liber VII. 1593. Reprinted
in New York: Georg Olms, pp. 398-400 and 436-446, 1970.
in New York: Georg Olms, pp. 398-400 and 436-446, 1970.
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England:
Penguin Books, 1986.
Penguin Books, 1986.
Wolfram Research, Inc. "Some Notes On Internal Implementation: Mathematical
Constants." http://reference.wolfram.com/language/tutorial/SomeNotesOnInternalImplementation.html.
Referenced on Wolfram|Alpha: Pi FormulasConstants." http://reference.wolfram.com/language/tutorial/SomeNotesOnInternalImplementation.html.
CITE THIS AS:
Weisstein, Eric W. "Pi Formulas." From
MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/PiFormulas.html
MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/PiFormulas.html
Εγγραφή σε:
Αναρτήσεις (Atom)