Harmonic Mean in Geometry
Harmonic Mean in Geometry
The
harmonic mean H(a,b) of two positive numbers
a and
b is defined as
H(a,b)=21a+1b,
and equivalently
2H(a,b)=1a+1b,
or else
H(a,b)=2aba+b.
It makes a most dramatic appearance in the
problem of average speed, but also pops up in various geometric circumstances. Below I collect a few examples.
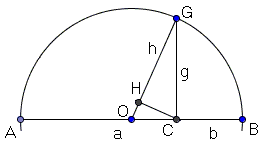
Let AGB be a semicircle and AC=a, BC=b.
If CG⊥AB and CH⊥OG then GH=H(a,b).
In a trapezoid ABCD, let EF be the line parallel to the bases AB and CD through the point of intersection of the diagonals AC and BD:
If CD=a and AB=b, then EF=H(a,b).
It is worth observing that the point of intersection of the diagonals divides EF into two equal parts, which leads to another common example:
In a 1877 sangaku from the Hyogo prefecture, AE and BD are both perpendicular to AB. P is the intersection of AD and BE, and CP⊥AB.
If AE=a and BD=b, then CP=2⋅H(a,b).
The same motif reemerges in the See-Saw Lemma where AE, BF, and EF are tangent (the latter at X) to the semicircle AXB.
If AE=a and BF=b, then XY=H(a,b).
Vladimir Nikolin from Serbia has observed appearance of the harmonic mean in his Rhombus Lemma.
Let AD be the bisector of ∠A in ΔABC, B′D||AC and C′D||AB. Then AB′DC′ is a rhombus and its side p is half of the harmonic mean of sides b=AC and b=AB.
Choosing the angle at A to be right leads to a special case where the rhombus becomes a square.
Let a square be inscribed into a right triangle as in the diagram
Then, if a and b are the legs of the triangle and p the side of the square, 1p=1a+1b. In other words, p=12H(a,b).
As a consequence of the Rhombus Lemma there is a simple way of constructing the harmonic ratio:
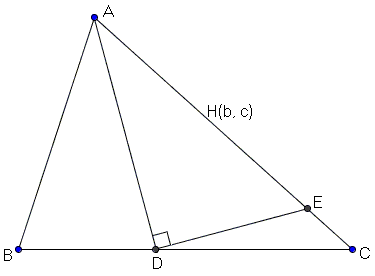
In ΔABC, with AB=c and AC=b, draw AD - the bisector of ∠A. At D erect a perpendicular to AD and let E be its intersection with either AB or AC. Then AE=H(b,c).






Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου